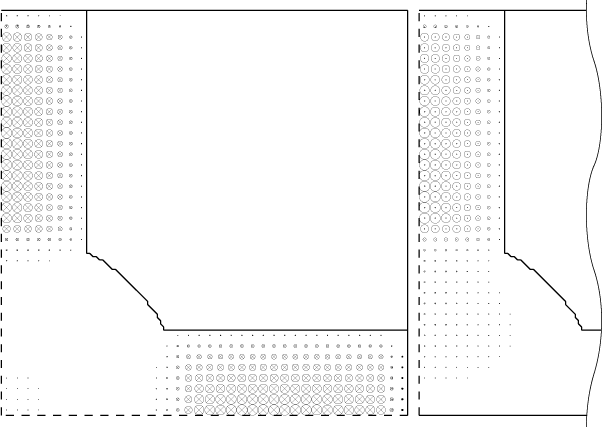
MAFIA[3]-simulation of the coupler cell:
monopole-like waveguide mode at 4.1682 GHz
and dipole mode at 4.1115 GHz.
Click here to take a look on the poster (MO4064).
To preserve the required beam quality in an e+/e- collider it is necessary to have a very precise beam position control at each accelerating cavity. An elegant method to avoid additional length and beam disturbance is the usage of signals from existing HOM-dampers. The magnitude of the displacement is derived from the amplitude of a dipole mode whereas the sign follows from the phase comparison of a dipole and a monopole HOM. To check the performance of the system, a measurement setup has been built with an antenna which can be moved with micrometer resolution to simulate the beam. Furthermore we have developed a signal processing to determine the absolute beam displacement. Measurements on the HOM-damper cell can be done in the frequency domain using a network analyser. Final measurements with the nonlinear time dependent signal processing circuit has to be done with very short electric pulses simulating electron bunches. Thus, we have designed a sub nanosecond pulse generator using a clipping line and the step recovery effect of a diode. The measurement can be done with a resolution of about 10 micrometers. Measurements and numerical calculations concerning the monitor design and the pulse generator are presented.
To explain the principle of operation, we take a look to the modes of
a single pillbox resonator. On the one hand, the monopole modes have a nearly
constant longitudinal electrical field near the axis. Therefore their excitation
by a bunch of charged particles does not depend on the displacement. The
amplitude after a passing of a bunch is proportional to the charge of the
bunch, the starting phase is independent of the displacement. On the other
hand, the dipole modes have no longitudinal electrical field on the axis.
Off-axis the field rises with the first Bessel function. Near the axis,
the amplitude after a passing of a bunch is proportional to the magnitude
of displacement and the charge, the starting phase (0°/180°) depends
on the sign of the displacement.
So we can use the complex amplitude of a dipole mode to measure the absolute
beam position in one azimuthal direction. A higher monopole mode serves
as a phase reference to detect sign of bunch displacement. The accelerating
mode is not useful for this purpose since amplitude is dominated by the
klystrons.
One possibility for the choice of a suitable monopole mode is the TM011
pillbox mode. Due to the fact of different frequencies of the TM011
and TM110 mode phase comparison of both modes is very difficult.
This method was described in a preceding paper [1].
To simplify the method it is desirable to have the same frequency for both
modes. This would simplify the synchronisation with the bunch and reduces
the number of intermediate frequency stages which leads to a considerable
reduction of costs. Thus one needs an additional monopole-like mode with
the frequency of the TM110 dipole mode. This is ensured by the
presence of reflections in waveguide corners of the HOM-damping system attached
(see for example the SBLC [2] HOM-damping
system).
|
| Figure 1: MAFIA[3]-simulation of the coupler cell: monopole-like waveguide mode at 4.1682 GHz and dipole mode at 4.1115 GHz. |
One suitable mode was found by a MAFIA-simulation (eigenmode solver) of the coupler cell closed by electrical boundaries within the iris and waveguide flanges. The mode on the left hand side of Figure 1 is the desired monopole mode with electrical field on axis. On the right hand side one sees the dipole pillbox mode geometry changed by the damping system attached. Due to the strong damping effect on both modes, the resonance curves are widely overlapped. Thus one can choose a frequency near both resonances. To proof the existence of the monopole mode and their coupling to the beam a MAFIA time domain simulations have been done.
For the measurements the beam was simulated by a movable antenna nearby the axis. Therefore a positioning system has been build with a mechanical resolution of 1.23 micrometers. As long as all components of the signal processing electronics are linear and time invariant, the measurements can be done in frequency domain. During the measurements the RF-source was connected to the movable antenna. The signals of the modes were detected by two pick-up antennas mounted in the waveguides of the damping system. The separation of monopole and dipole signals were done by a 180° ring hybrid which delivers the sum and the difference of the signals.
|
| Figure 2: Transmission from antenna to Sum- and Delta-Port at 4.198 GHz in dependence of the displacement. |
Figure 2 shows magnitude and phase
of the transmission from the movable antenna (A-Port) to the Sum- (monopole
signal) and the Delta-Port (dipole signal) of the hybrid depending on the
position of the input antenna. As expected, the dipole signal rises linearly
with the magnitude of displacement and the phase between monopole and dipole
signal jumps by 180° at zero displacement. Furthermore the result shows
a much stronger coupling to the monopole than the dipole mode. Even at positions
far off axis (1.5 mm) the monopole transmission is two times the dipole
transmission. Thus it is clearly shown that the 180° ring hybrid is
necessary.
Figure 3 shows the ratio of dipole to
monopole transmission in magnitude and phase with the maximum resolution
of the positioning system. This measurement was performed at optimum frequency
of 4.197 GHz. We found a phase jump within 1.23 micrometers on
axis. Apart from the optimum frequency the minimum is flatter and is further
away from zero. Due to the fact of mechanical tolerances of the damping
system, the electrical axes of the monopole and the dipole modes are different
(Figure 2). Thus the electrical field
of the monopole mode is not constant near the axis of the dipole mode. Together
with the limited isolation of the hybrid the signal is not symmetric, which
causes a relative inaccuracy of 6 % of the beam displacement.
|
| Figure 3: Transmission ratio at 4.197 GHz in dependence of the displacement. |
Further measurements with the nonlinear time dependent signal processing circuit have to be done with very short electric pulses simulating electron bunches.
The requirements to produce a short pulse are small transition time and small pulsewidth. A 10 MHz oscillator pulse is shaped by a clipping line and the transition time is shortened by a step recovery diode. The pulse generator is realized on a single microstrip line printed circuit board completely. The schematic configuration is shown in Figure 4.
|
| Figure 4: Schematic of a fast pulse generator (simplified). |
Measured output signal of the pulse generator inThe step recovery diode
can be described as fast switch reducing the fall time of the oscillator
pulse. A forward bias IF stores charge and the negative oscillator pulse,
powered by two V-MOSFETs, causes a reverse bias IR which depletes this charge,
and when fully depleted the step recovery diode ceases to conduct current.
The action of turning off takes place within 100 ps or less depending on
forward and reverse bias and the specific carrier life time of the diode.
The clipping line changes the falling edge into a pulse, and pulse length
is given by two times the delay of the clipping line which has to be longer
than two times the rise time of negative edge. Otherwise the resulting pulse
height decreases. To avoid multiple reflections the entrance of the clipping
line, seen from the short end, should be matched. But due to presence of
the diode capacity and parasitic inductances of the MOSFETs perfect matching
is impossible. The effect of multiple reflections on the resulting pulse
can be seen in Figure 5 , after the desired
negative pulse, which ends around 800 ps, the signal is oscillating
around zero.
|
| Figure 5: Measured output signal of the pulse generator in Figure 4. |
One possibility to get rid of the undesired multiple reflections caused by the mismatch of the clipping line is to connect the diode directly to the common drain of the MOSFETs. The disadvantages are now the parasitic inductances and capacities of the MOSFETs which influence the pulse stronger than before. On the other hand due to the inductances the pulse height is increased. Additionally length and impedance of the clipping line were optimized to achieve a more proper pulse. This is ensured by destructive interferences eliminating the parasitic oscillations. Furthermore leading parasitic oscillations can be minimized using a second line with an open end. All these precautions were verified numerically with the program SPICE [4] and are not yet realized experimentally. The configuration is shown in Figure 6 and the results are presented in Figure 7.
|
| Figure 6: Schematic of a optimized pulse generator (simplified). |
|
| Figure 7: Calculated output signals of the pulse generator in Figure 6. |
The resolution of the HOM-damper beam position monitor is limited by
strongly excited monopole modes. It has been shown that a resolution of
10 µm seems possible. The relative inaccuracy caused by the axes
offset of the monopole mode, which is in the order of 6 %, can be decreased
by the construction of a new HOM-damping system which can be machined more
precisely. Furthermore an inaccuracy due to the evanescent accelerating
mode in the HOM-damping waveguides is expected. But this influence depends
strongly on the signal processing electronics and has not yet been proven.
For measurements with the pulse generator the new proposed setup (Figure 6) will be built and tested.
This concept of a beam position monitor can be applied to any high energy
cavity type linac with symmetric HOM-damping system. Due to the synchronisation
with a higher monopole mode, external synchronisation to the timing system
of the linac is not necessary. Thus beam position monitoring is also possible
in non accelerating cavities.
[1] C. Peschke, P. Hülsmann, H. Klein, W.F.O. Müller: "Beam Position Monitoring for SBLC Using HOM-Coupler Signals"; proceedings of the 5th European Particle Accelerator Conference (EPAC 96); Sitges (Spain), 1996
[2] R. Brinkmann et al.: "Conceptual Design of a 500 GeV e+/e--Linear Collider with Integrated X-Ray Laser Facility", DESY 97-048, Hamburg (Germany), 1997
[3] T. Weiland et al.: "Solutions of Maxwell's Equations using the Finite Integration Algorithm"; Version 3.2; Darmstadt 1993
[4] "Simulation Program with Integrated Circuit Emphasis"; Version 3f4; Department of Electrical Engineering and Computer Science, University of California, Berklay, California 1993
* Work supported by DESY/Hamburg and BMBF under contract 06OF841
[ Up | Linear Collider Page | IAP Page | Physics Page | JWG Uni Home ]